Osnovna je osnova za sva učenja koja poznaju svijet matematika. Točna znanost koristi formalizirani jezik te proučava redoslijed, strukturu i odnose na odabranim apstraktnim objektima. Ne vole svi učenici matematiku zbog nje složenost i zbunjenost, ali najvjerojatnije zato nesporazum. Trajne promjene u odnosu na matematiku zahtijevat će predanost, koncentraciju, dosljednost, čak tvrdoglavost i, što je najvažnije, praktična rješenja. U studiji je važno korak po korak razumjeti jednostavno i postupno prijeći na složenije, ne ostavljajući ništa nerazumljivo i loše osmišljeno.
Postoji mnogo različitih grana matematike koje su dovoljno proučavane i pojavile su se nedavno. Sljedeće opisuje osnove matematičke analize - osnovne početne koncepte, definicije i pravila za proučavanje jednostavnih funkcija jedne varijable, derivacije i diferencijacije.
Aforizam je nastao među osnovnoškolcima: "Matematika postaje stvarno komplicirana kad iz nje nestanu brojevi." Dapače, oni se približavaju razumijevanju nekih definicija i zakona matematičke znanosti odlučivanjem o pravilima koristeći konkretne primjere..
Ključne definicije
Započnimo s terminologijom - jednostavnim općim semantičkim značenjima primarnih definicija:
- varijabla - vrijednost ili simbol, može uzeti bilo koju od niza vrijednosti u
određeno područje (težina ili visina djeteta)
- funkcija - svrhu, rad, aktivnost, specifično djelovanje na varijablu, označavamo f (x) (ovisnost težine djeteta o njegovoj visini)
- granica - granica, rub, rub (horizont - vidno polje)
- derivat - formirani, sekundarni, teče iz drugog, označavamo f '(x) (brzina pri kretanju)
- diferencijal - razlika, razlikovanje, odvojenost.
Funkcija je pravedna
Funkcija je rezultat onoga što čini sa varijabli, što je rezultat izračuna. Ovo je odnos elemenata u kojem promjena jedne varijable uzrokuje promjenu u drugoj. Podijelite f (x) na jednostavne i složene.
Sljedeće metode koriste se za prikaz ovisnosti: algebarske, grafičke, tabelarne, logičke, pa čak i softverske.
Numeričke ovisnosti određuju se algebralno korištenjem simbola varijabli, jednakosti i nejednakosti (≤ i>), konstruira se jednadžba oblika: y = f (x), ovdje je x varijabla ili argument, a y ili f (x) je funkcija. Za svaku specifičnu vrijednost varijable x iz dopuštene domene definicije odgovara određena vrijednost y za dati f (x).
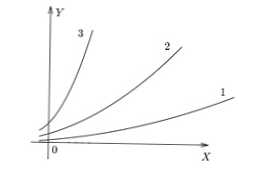
Na slici ispod prikazani su jednostavni grafovi u 3 različita omjera. Može se vidjeti da je u f (x) 3 najveća vrijednost y dobivena za x specifična, u f (x) 1 - najmanja.
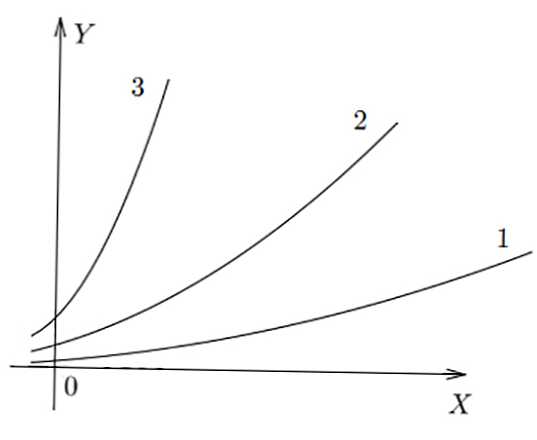
funkcija
Razlikuju se sljedeći elementarni izrazi: linearni (izravni), kvadratni (parabola), kubični, hiperbola, eksponencijalni, logaritamski, trigonometrijski (prikazano u donjoj tablici).
Za analizu svakog tipa f (x) određuju se njihova svojstva (navedena u nastavku), a za to se koriste koncepti izvedene i diferencijalne.
Derivativna funkcija
derivat - operater, koji za izvorni f (x) prema zakonima diferencijacije pridružuje drugu funkciju, ona karakterizira promjenu primarnog f (x) argumenta x u nekom trenutku. Za njegovo detaljnije razumijevanje trebalo bi se pozabaviti složenijim definicijama granice ovisnosti i diferencijacije..
granica - ta je definicija dinamična. Izraz koji x teži ka n razumijeva se na sljedeći način: x stječe vrijednosti koje su blizu n i razlikuju se malom količinom.
diferencijal - mala promjena neke veličine. Priraštaj se naziva delta.
Derivat za f (x) u točki je granica dijeljenja delte funkcije s delta varijable u određenoj točki, ako posljednja teži 0.
Karakteristika brzine promjene ovisnosti u određenoj točki, geometrijski se može prikazati kao tan vrijednost kuta nagiba alfa tangenta u funkciji.
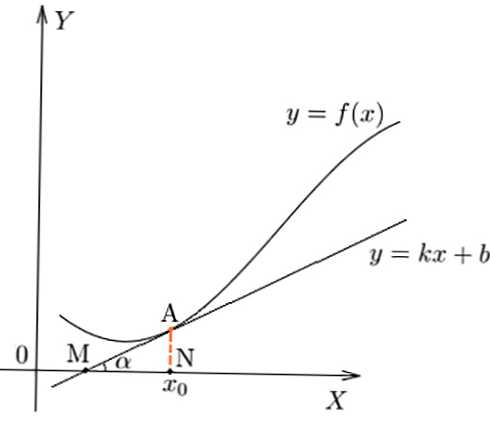
derivat
Zavisnost se naziva diferencibilnom ako je definirano f '(x). Pronalaženje derivata naziva se diferencijacijom. Pravila za izračunavanje f '(x) i podudaranja f' (x) iz elementarnog f (x) su dana u donjoj tablici
I izvedena funkcija funkcionira
Svaka ovisnost ima određena svojstva, znajući i istražujući ih možete analizirati prirodu stanja i promjene f (x).
Glavna svojstva:
- Podaci o definiciji i vrijednosti.
- Nula (x)
- Funkcija se u nekim intervalima povećava ili smanjuje.
- Bodovi MAX i MIN funkcije, postoji li pomak.
- Neparni ili neparni f (x)
- Ograničena i neograničena funkcija.
- Postoje li asimptote.
- Frekvencija f (x).

Funkcije i derivati
Pri uspostavljanju karakteristika ovisnosti pomoću derivata koriste se međusobne veze svojstava f '(x) sa svojstvima f (x) i obrnuto. Karakteristike f '(x) lako se određuju na grafikonu funkcije, i obrnuto, karakteristike primarnog f (x) razumiju se iz grafikona f' (x). Ispravljajući suštinu svake značajke funkcije, istražite i uspostavite lanac odnosa. Za određivanje asimptota u grafovima koristi se pojam ograničenja..
Ispod su neke karakteristike i ovisnosti f '(x) o f (x):
- Kako se f (x) povećava u intervalu, f '(x) je pozitivan.
- Ako se f (x) smanjuje tijekom intervala, f '(x) je negativan.
- U prisutnosti f (x) točka MAX, f '(x) = 0 u njoj se ne može odrediti, a tg kuta tangenta mijenja znak iz + u -.
- U prisutnosti f (x), točka MIN, f '(x) = 0 u njoj se ne može odrediti, a tg kuta promjene tangente mijenja se iz - u +.
- Pri savijanju f (x) u E, vrijednost f '(x) nije promijenila znak u točki, f' (x) = 0.
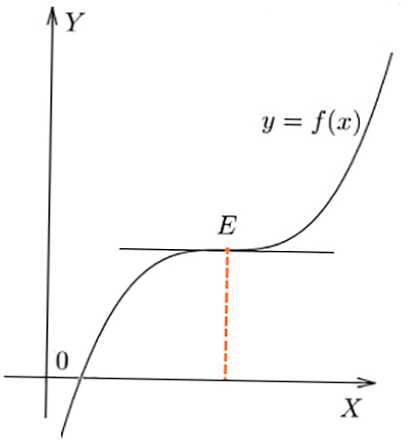
Flekcija u točki E grafikona funkcije
Za istraživanje, f (x) čine shemu u kojoj je svaki korak konstruiran prema specifičnom algoritmu za proračun i analizu odnosa komponentnih elemenata.
Razlike u funkciji i izvedenici
Pravila zbrajanja i oduzimanja f (x) ista su kao i pravila tih radnji tijekom diferencijacije. Ali pravila za pronalaženje f '(x) pod radnjama množenja i podjele funkcija su različita (kao u tablici).
Funkcija je primarna, a izvedenica je sekundarna matematička operacija, a u većini slučajeva imaju različite karakteristike.
Točka neprekidne zavisnosti koja se sabire nalazi se njezinim drugim derivatom, a njezin znak treba se mijenjati u regiji točke x0.
Postoje takve vrste funkcija koje nemaju f '(x) u točki x0 (diskontinuirano). U izrazu ln (| x | -1) derivat nije definiran u točki x0 = 1.
Postoje izrazi "Modulo" slično y = | x |, koji ima kink u x0.
Za takve ovisnosti koriste se samo djelomično (u intervalima definicijske domene) metode proučavanja njihovih svojstava pomoću derivata i nije uvijek moguće prebaciti sa svojstava f '(x) na svojstva primarne.
Nigdje se ne može učiniti bez iznimke od pravila, pa čak ni u matematici. Da bismo analizirali i konsolidirali predstavljeni materijal, neophodno je riješiti primjere, vježbati, steći iskustvo s ograničenjima, diferencijalima i izvedenicama i hrabro prijeći na integrale.











